This is the first lecture of Political Science and International Relations (Optional) Aug 2018 Batch by Shubhra Ranjan.
Next Batch starts on 28 Oct 2018 For admissions Visit our. Website : http://shubhraranjan.com
(Admissions open for PSIR Oct Batch, Only10% seats remaining.)
Classes are held in Delhi & Live Classes are available in Pune centre.
source













![CY_GATE_2019_PHYSICAL_SPECTROSCOPY_[ELECTRONIC_BASIC]_All IN ONE_[Short_Trick]_2018-19_PART_1ST - Videos](https://trends.edugorilla.com/wp-content/uploads/sites/8/2018/08/cy_gate_2019_physical_spectroscopy_electronic_basic_all-in-one_short_trick_2018-19_part_1st-218x150.jpg)








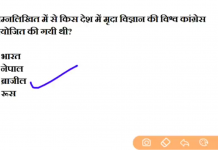






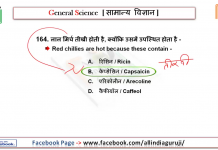


![24 August 2018 – The Indian Express Newspaper Analysis हिंदी में – [UPSC/SSC/IBPS] Current affairs - Videos](https://trends.edugorilla.com/wp-content/uploads/sites/8/2018/08/a520-218x150.png)





Mam u should also take live classes for peoples who live far from delhi
thanks mam
Ma'am please provide paid online classes for political science optional. Then only all aspirants got good teacher like you. Thank you so much ma'am.
Ma'am will you provide online class for political science
Mam pls upload part 2 and other remaining parts of the full course lecture on PSIR Preparation on this channel.
Thanks mam…. N plse do upload all Ur lectures of PSIR ….so that everyone who do not afford classes could do study far from delhi🙏🙏🙏🙏🙏……
Thanks
dear team who will take geography
optional,his/her experiences etc
I miss her classes
Is it paid one or free one?
I have really no word to think but being a human I only say to u mam ur just great. Please continue these online classes so that we poor people can benefit from it and reach the destination. Thanks 🙏🙏🙏🙏 mam
plz start online batch
Mam delhi mein padai na kar pane vale hum students ki taraf se bahut bahut dhanyavad mam please continue it…
Mam teach both optional paper 1 and paper 2 from online..lots of love from Hyderabad
Start online telecast in Jaipur too..like visionias…willing to pay full fee.. can't come to delhi
Mam plz complete this course for political science and ir optional so we can also study from u it is humble request
Mam please provide all the lectures on you tube…We living far away from Delhi and Pune will be highly benefitted… We will be very much thankful to u for this generosity..
Thnk u so much mam
How I can I purchase your note mam
ma'am plz also start the online classes so that people who are far away also could attain the class.
Please tell the way also for students who are unable to attend your coaching. Mam please guide me I will be very thankful for your generous help, please upload video at least on important topics, I can understand that you can't give free lectures but can render valuable guidance for poor students like me who are studying on free rail WiFi and public library.
Please do a needful.
I hope you understand the need of students.
Very nice mam
Mam please make it online course like this…I am ready to enroll..and I hope lots of many aspirant wants to access to such a quality course online …thanks mam
thanks for this amazing video mam….this is my humble request to u that please provide us your all videos concern with political science.
Very Nice, would you consider using my music for free? Love to see more!
plzz upload more lectures
Thanks Ma’am, I am going to join in the new batch of June 2019
Thanks mam
RESPECTED MADAM THANKS
Thanks ma'am please do upload for PSIR(optional) it will be helpful for students who live in remote area like me
Those who r not affordable
For them u r doing this on
YouTube channel
U r really great mam
I'm grateful 2 u mam
Please continue this channel
It's 100 % worthy for
Poor ias aspirants
Political optn ke liye book bta do koi hindi me???? Plzzz
is this for optional or…
Please upload videos of everyday classes…so that we can study and complete the paper with the classes going on….it will be of great help to us
Nice madam , Please start online paid classes. Atleast for paper 1. It will be helpful for everyone especially those students who are not in delhi.
Thank you very much for the guidance ma'am… Even though I'm not your student I feel I'm one of your students…Very inspiring and motivating… Thank you ma'am